Balancing games is difficult, but difficult problems are fun. In this post, I’ll dig into some of the maths behind The Long Road.

The Long Road (TLR) blends elements of roguelike games and classic text-adventure. You play as a group of scavengers wandering a post-apocalyptic wasteland; collecting food, weapons, and more scavengers in a bid to survive. As you explore your world, you are presented with choices that shape the world around you and ultimately determine how long you will last. But, how long should that be?

A balancing act

There is tension in TLR. A cursed problem arising due to conflicting promises that we make players. We want players to make meaningful decisions, think strategically, and try to survive as long as possible. However, enabling the player to survive forever through skill alone renders the game boring. One popular way to solve this problem, is by injecting some randomness. Now players are a dice-roll away from thriving (or failing).

But how do we maintain this knife-edge? Give the player too much and their dice rolls become meaningless. Be too harsh and every run feels horribly unfair. To better understand how to successfully design TLR, we will need to dig into the numbers.

The dynamics of scavenging

There are three resources in The Long Road: food, weapons, and scavengers. Scavengers eat your food to survive: more scavengers need more food and without it, they die. Weapons enable combat options in conflicts — outcomes are better with them than without… The game ends only when you run out of scavengers.

TLR is turn-based, allowing the player to choose one of four directions to move in during each turn. Each new tile you explore may give you either some resources, a conflict, or nothing at all. At the end of the turn, your scavengers consume some of your food (or starve and die). The Long Road includes a healthy serving of randomness, but we want to know how long the player should expect a game to last. Let’s start with some simple first steps.

Wanderers, not yet scavengers

For now, forget about the randomness and look at a simplified problem. If scavengers found no resources, how long would they last on the long road?

Let \(X_t\) be our food at the start of turn \(t\), and \(Y_t\) be our scavenger count. Each scavenger consumes \(\alpha > 0\) food per turn. Remember, the game runs out when the last scavenger dies (\(Y_t < 1\)). In this simplified version of TLR, the food changes each turn using the following rule,

\[X_{t+1} = \max(X_{t} - \alpha Y_{t}, 0).\]

Additionally, each excess unit of food that is consumed leads to a scavenger’s death:

\[Y_{t+1} = Y_{t} + \min(0, X_{t} - \alpha Y_{t}).\]

This is already looking pretty complicated, but we can make better sense of this by picking some specific values. If we take \(\alpha = 0.5\) for example, then in each turn we consume food equal to half of our scavengers. And if we have zero food left, then half of our scavengers die each turn.

The quantity we care about here is how many turns we can last before we hit game over, i.e., the smallest \(t\) with \(Y_{t} < 1\). First, how many turns before we run out of food? This is given by \(X_{0} / (\alpha Y_{0})\). After this point, the scavenger count evolves like,

\[Y_{t} = (1 - \alpha) Y_{t-1} = (1 - \alpha)^{t} Y_0.\]

Now notice that if \(\alpha \geq 1\), then it takes only one turn for all of the scavengers to starve to death once the food has run out. If the scavengers ration better (\(\alpha < 1\)), then we need,

\[t > \frac{- \log(Y_0)}{\log (1 - \alpha)},\]

turns for all of the scavengers to starve (\(Y_t < 1\)). So the total number of turns is roughly,

\[\frac{X_{0}}{\alpha Y_0} + \frac{- \log(Y_0)}{\log (1 - \alpha)}.\]

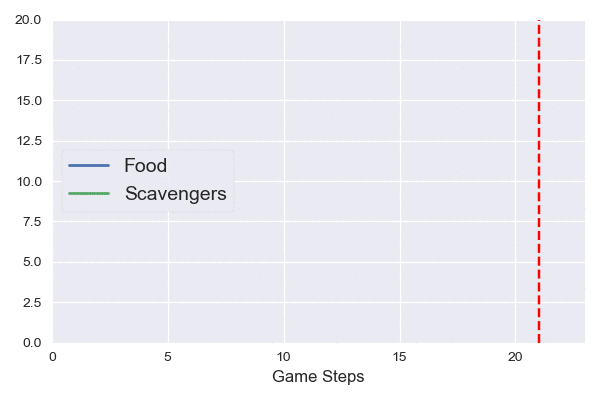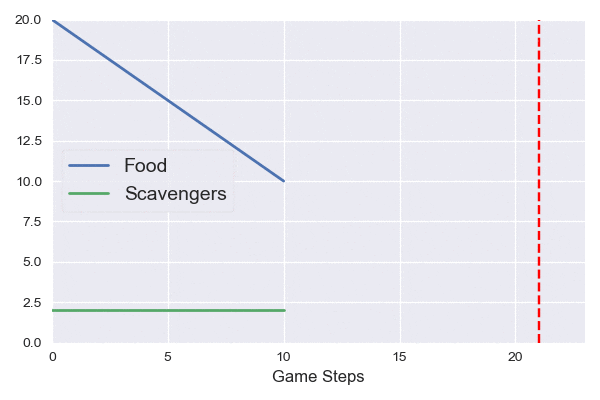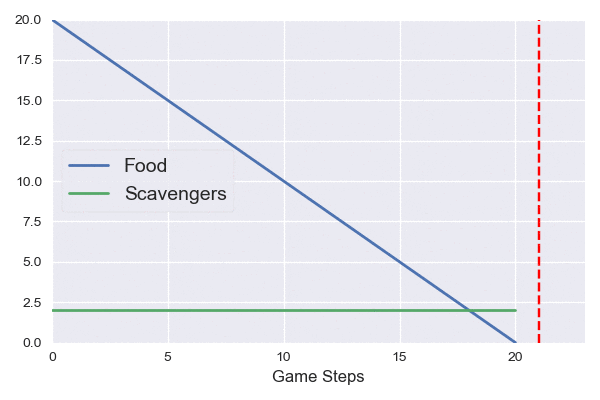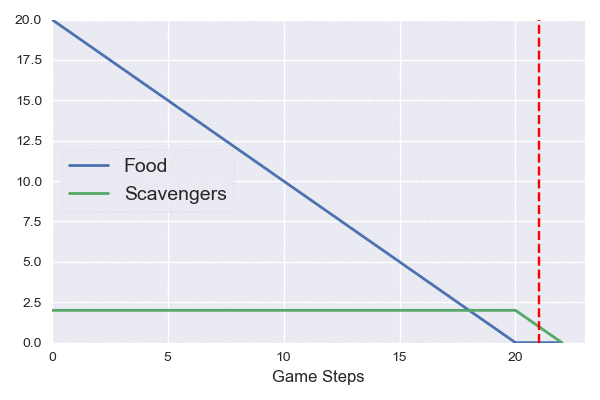
Looking at this quantity, we see that adding more scavengers decreases the total number of turns. While adding more food increases it. On the other hand, as scavengers get more greedy (\(\alpha\) increases) then they last fewer turns.

The animation on the left simulates our boring survival game. Food decreases at a fixed rate until it runs out and the scavenger dies. The red vertical line indicates our predicted stopping point (the first time when the scavenger count is <1).

Scavengers

Let’s make things slightly more interesting. Now our scavengers have learned that to survive they need to find more food, and friends. In each turn, scavengers find \(C > 0\) more food, and \(K > 0\) new scavengers join the group. The group then consumes the food at rate \(\alpha < 1\) per scavenger. Our new food dynamics are given by,

\[X_{t+1} = \max(X_{t} - \alpha (Y_{t} + K) + C, 0).\]

Each turn, scavengers consume food — including the \(K\) new friends we found — but we also gain \(C\) new food. Similarly, the scavenger dynamics become,

\[Y_{t+1} = Y_{t} + K + \min(0, X_{t} - \alpha (Y_{t} + K) + C).\]

We gain the \(K\) new scavengers, but we may also lose some scavengers to starvation. How many turns can the scavengers last now?

First, notice that if \(C > \alpha (Y_t + K)\) then the scavengers gain food on each turn. But the number of scavengers is always increasing by \(K\). The scavengers will stabilize when \(X_{t} - \alpha (Y_t + K) + C = -K\). When this condition holds, we also have \(X_t = 0\). Solving these together, we get the equilibrium point,

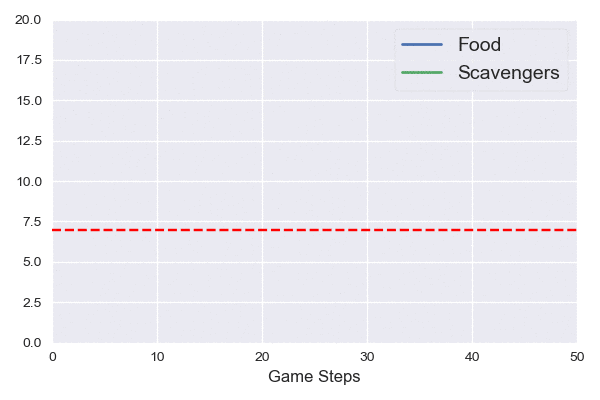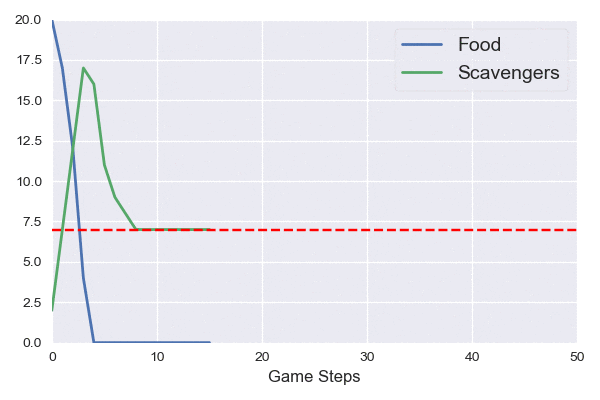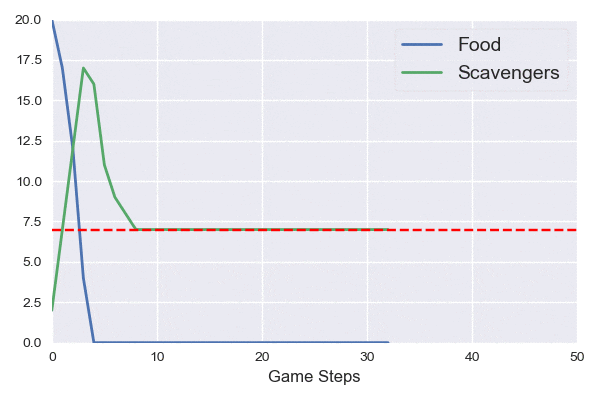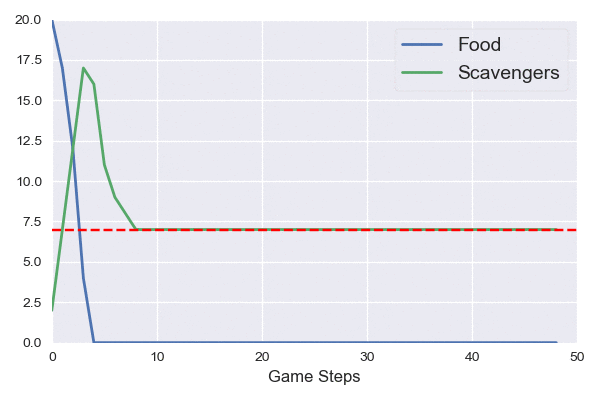
\[X^* = 0, \hspace{2cm} Y^* = \frac{C + K}{\alpha} - K.\]

On the right, we see a simulation of these dynamics. The red horizontal line indicates the stable point for the scavengers, which is reached before 10 steps.

So long as \(\alpha < (C + K) / K\) (this is always true when \(\alpha < 1\)), each turn some scavengers die and are replaced anew. But sadism aside, this isn’t very exciting for the player — they can never lose! How can we fix this?

Scavengers scavenge, sometimes

Instead of giving a constant amount of food and scavengers to the player, let’s make each of them random. With probability \(p < 1\) the player gains \(C\) food, with probability \(q < 1 - p\) the player gains \(K\) scavengers, and otherwise nothing.

Our dynamics are now stochastic, meaning sometimes things go up and sometimes they go down. They also form a Markov chain; the present state tells us everything that we need to know about predicting the future.

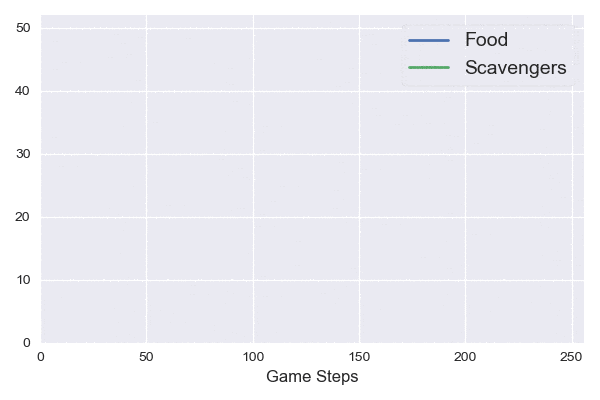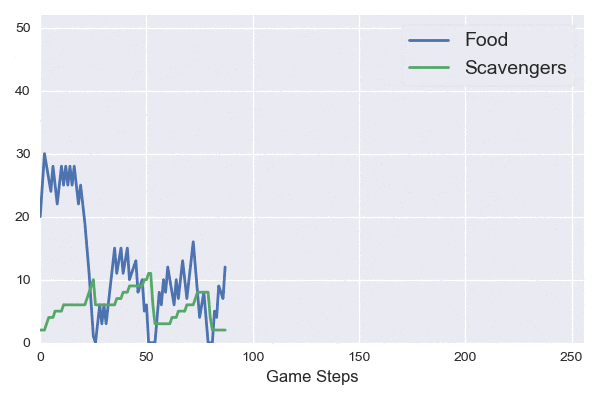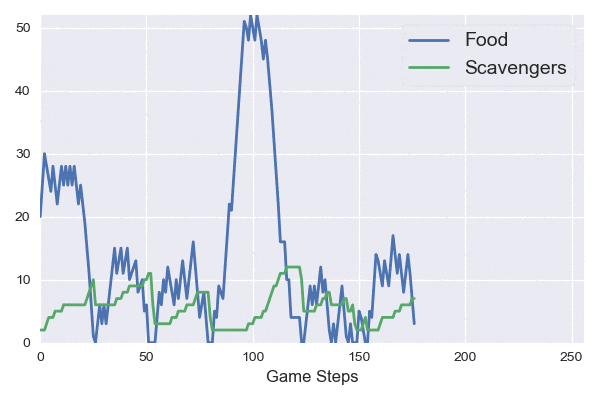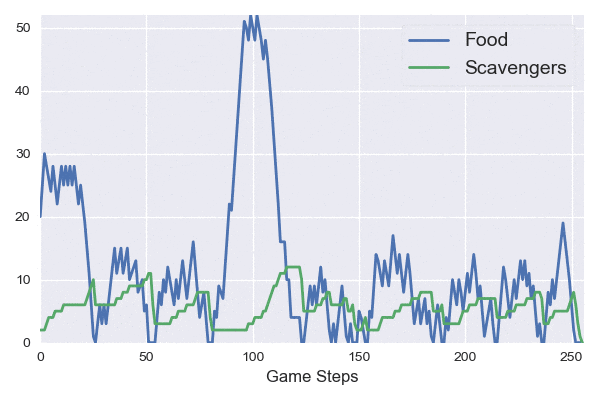
This leads to much more interesting dynamics.

The stochastic dynamics are significantly more complicated than the deterministic cases before. We now care about a random variable: the stopping time of the process (when the number of scavengers goes below 1). We need to reason about this random variable in terms of its distribution or moments, e.g. the expected value. I’d love to say more about this, but I haven’t figured it out yet… Let me know if you have any ideas or a reference that might help!

Regardless, being able to simulate these systems lets us estimate the stopping time and figure out how tweaking parameters under the hood of our game will affect the average run time and variance within. This is powerful when it comes to balancing — we can instantly simulate a simplified run of the game and get an idea of how long things should last.

What is left?

In this post, we explored only a simplified version of the game. However, the dynamics that we explored are close to the ones we utilize in TLR. [There are a few differences and maybe I’ll explore these in a future post…] On the other hand, we completely ignored several important components that make up our game.

Conflicts

Instead of gaining a random amount of resources, players might find themselves faced with a conflict in which they must decide what to do. The outcome from their choice is random, and can range from wonderful to catastrophic. Weapons become useful during conflicts, where they unlock additional choices that are more likely to have favourable outcomes.

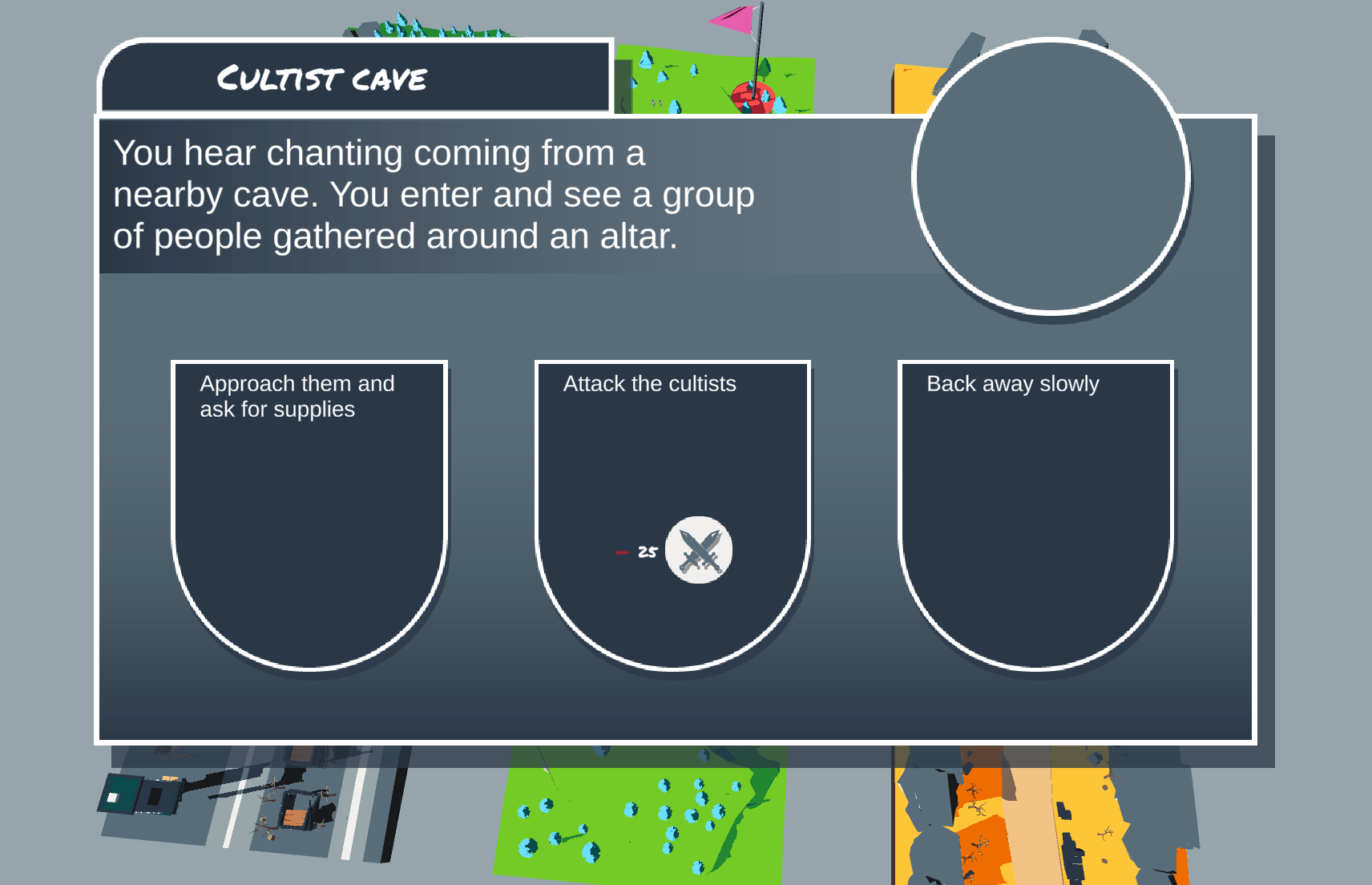
Conflicts are an additional layer of complexity in TLR’s dynamics, and also provide the player with greater agency — something that good balance should take into account. We want the player to feel that they are making meaningful decisions that impact their fate while maintaining that knife-edge balance.

Biomes

In addition to our three resources, TLR has three different biomes to explore. Each has its own set of rules governing how the player’s resources change. Forests provide the player with more food but fewer weapons. The wastelands provide very few resources but are generally low-risk. And the cities provide plentiful resources, but have a high chance of dangerous conflicts.

Balancing around the biomes is also tricky. We want to encourage the player to move strategically between biomes. One way in which we do this is by restricting conflicts to occur only in specific biomes, meaning the player will need to explore to uncover more of the story. Additionally, explored tiles don’t give any new resources/conflicts so that the player must keep moving. We are thinking hard about how the different dynamics in each biome can be combined to give well-balanced, meaningful gameplay.

Conclusion

This post only scratches the surface on balancing TLR. We showed, quantitatively, that randomness is needed to make the game interesting. Without it, the survival dynamics become predictable and unexciting. However, we will need to revisit these ideas and build out more complex models to make meaningful balance decisions.